This Article shows Past Questions and Answer workings in Numerical Methods for Higher National Diploma (HND) Students of Electrical/ Electronics Engineering Auchi Polytechnic, Auchi.
This Past Questions and Answers is helpful to all students in Engineering Technology offering Numerical Methods (MTH 321). For those currently writing their on going exams in Electrical Engineering HND 2 Power Option. This is the past questions and answers for you to study.
N.B – These questions and answers are uploaded only as a guide and ease for your studies.
FIRST SEMESTER EXAMINATION 2023/2024 ACADEMIC SESSION
DEPARTMENT: ELECTRICAL ELECTRONICS ENGINEERING CLASS: HND2
COURSE: NUMERICAL METHODS (MTH321).
DURATION: 2 HOURS 30 MINS
INSTRUCTION: ATTEMPT ANY FOUR (4) QUESTIONS
1a), Define iterative methods
(ii). Mention five types of matrices with an example
(b). Use iteration method, correct to 2 decimal places, to find the roots of the equation
f(x) = x³ = x² + x + 1
2(a) Use the square root iteration to find the square root of seven (7)
(b). Estimate the real root of the equation f(x) = x⁶-x-1= 0, up to three decimal places by Bisection methods- Stop after six (6) iterations.
3a) Write the Newton- Raphson procedure for finding ³√N, where N is a real number, use it to find ³√18 correct to 2 decimal places
3(b) Use the modified Jacobi’s method, solve the following system of linear equations
2X1 – X2 + 2X3 = 3
X1 + 3X2 +3X3 = -1
X1 + 2X2 + 5X3 = 1
Starting with the initial approximation x1 = 0.3, x2 = -0.8 & x3 = 0.3
4(a) Given a table of function f(x) as shown below, it is required to fit a polynomial that satisfies the set of points given.
(b) Mention six (6) errors committed in Numerical computation
5(a) Given a function f(x) =√x integrate and generate the values between the argument 1.0 (0.05) 1.30, rounded off five decimal places, using: (i) Trapezoidal rule (ii) Simpson 1/3 rule
(b). Show the end results of second back ward differences operator (V²yk)
6(a).Find by the method of REGULA FALSI, the root of the equation f(x) = x³ + x² – 3x – 3 = 0 lying between 1 and 2 to one decimal place.
(b), Perform two iteration of Picard’s method to find an approximate solution of the initial value problem
dy/dx = x+y²
y(0) =1
Study the Answers Available!
1(a) Iterative methods are algorithms used to solve mathematical problems, particularly linear systems, optimization problems, and differential equations, by repeatedly applying a fixed set of rules or operations to generate a sequence of approximations that converge to the solution.
(ii)
I. Identity Matrix: An identity matrix has all elements as 0 except the main diagonal, which has all elements as 1. Example: [1 0]; [0 1]
II. Zero Matrix: A zero matrix has all elements as 0. Example: [0 0]; [0 0]
III. Diagonal Matrix: A diagonal matrix has all elements as 0 except the main diagonal, which has non-zero elements. Example: [2 0]; [0 4]
IV. Upper Triangular Matrix: An upper triangular matrix has all elements below the main diagonal as 0. Example: [1 2]; [0 3]
VI. Symmetric Matrix Example: [2 3]; [3 2]
4(b) Errors committed in Numerical Computation
- Roundoff Error: Occurs when a numerical value is rounded off to a limited number of significant digits, leading to a loss of precision.
- Truncation Error: Happens when a numerical method is truncated or approximated, resulting in a discrepancy between the exact and approximate solutions.
- Overflow Error: Occurs when a numerical value exceeds the maximum limit of the computer’s memory, causing an incorrect result.
- Underflow Error: Happens when a numerical value is too small to be represented by the computer’s memory, leading to an incorrect result.
- Discretization Error: Occurs when a continuous problem is discretized into a finite number of steps, leading to a difference between the exact and approximate solutions.
- Propagation Error: Happens when errors from previous calculations are carried forward and amplified in subsequent calculations, leading to an inaccurate final result.
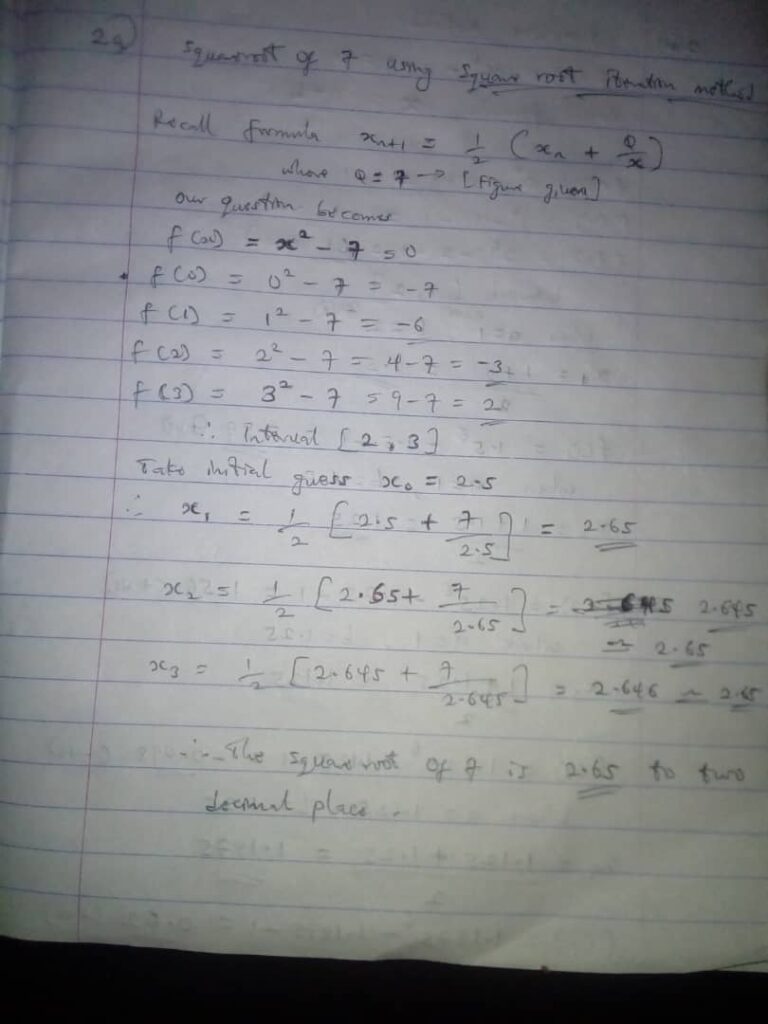
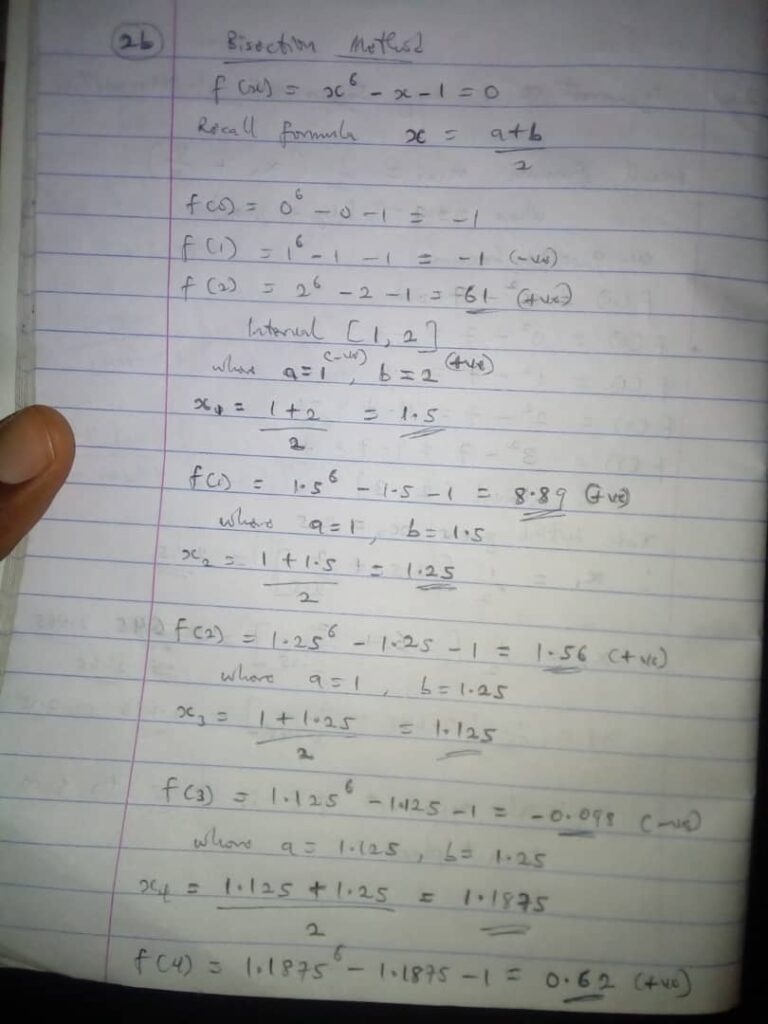

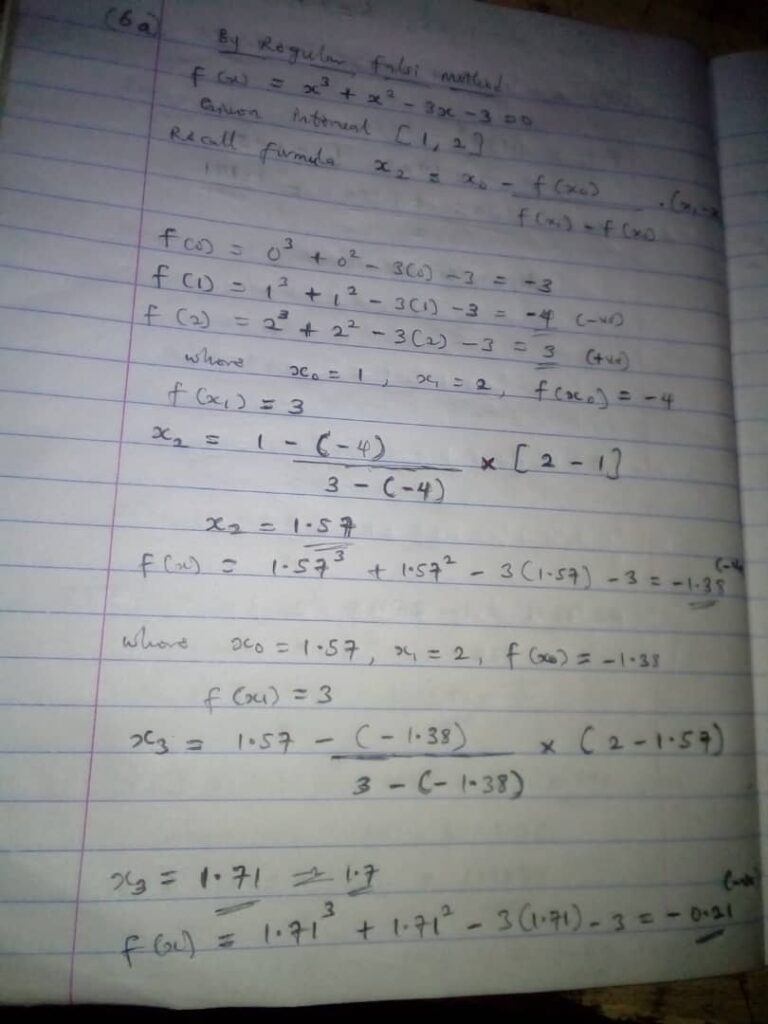
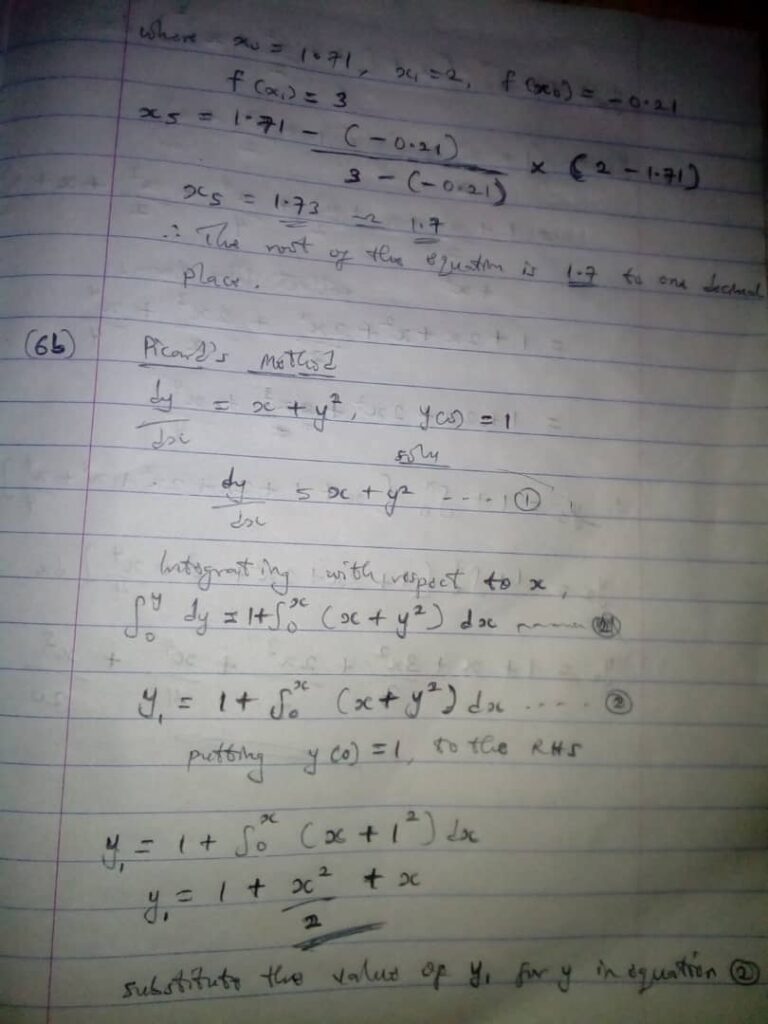
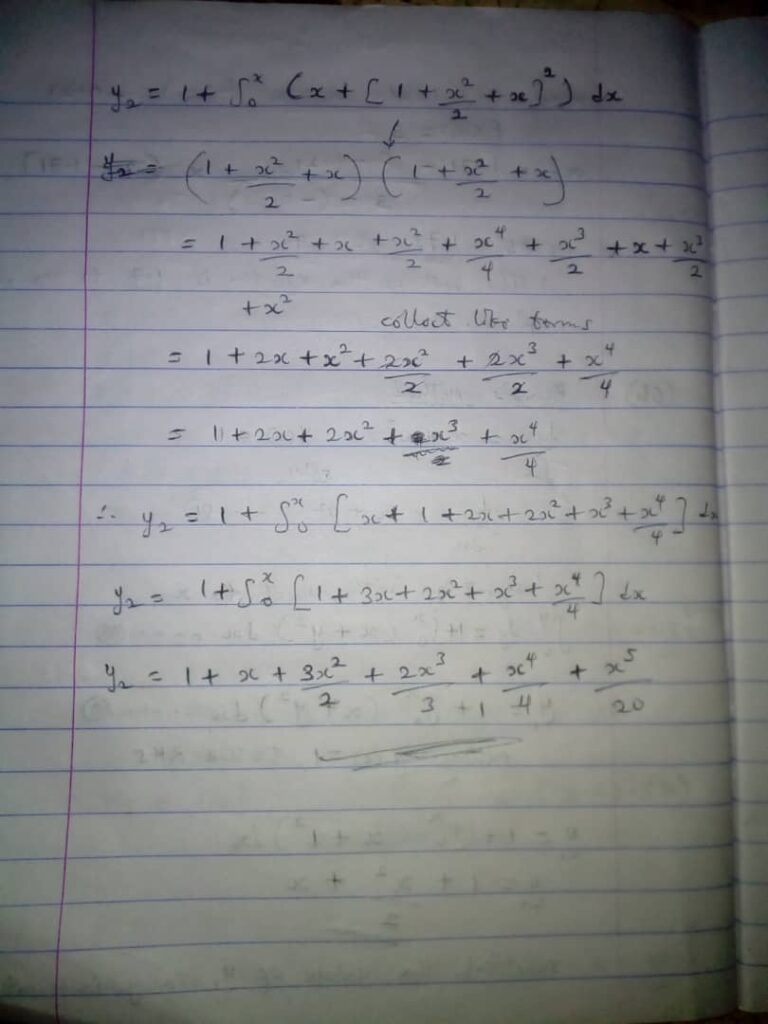
![]()

Very interesting information!Perfect just what I was looking for!Blog monry